服务热线
试卷总分:120分 命题人:dcyx2021 考试时长:120分钟
A.函数图象的开口向下
B.函数图象的顶点坐标是（-1，5）
C.该函数有最大值，最大值是5
D.当x＞1时，y随x的增大而增大
如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC=6，sinA=
，则DE的长为（ ）
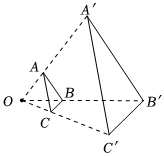如图，△ABC和△A′B′C′是以点O为位似中心的位似图形，点A在线段OA′上，且OA：AA′=1：2，若△ABC的周长为4cm,则△A′B′C′的周长为 cm.
的图象交于点A（1，m），与x轴交于点B，与y轴交于点C．图象上一点，S△OBP=2S△OAC，求点P的坐标．
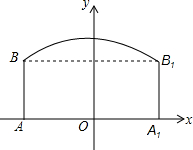如图，隧道的截面由抛物线和长方形构成，长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.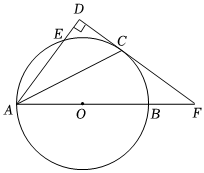
dcyx2021
2024-10-16
初中数学 | 考试 | 难度:1.5
word试卷生成中,请等待...
x
解析
收藏
下载
相似
组卷
如图是一个空心圆柱体，其主视图是（ ）
如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（ ）
=
如图，四边形ABCD内接于⊙O，∠C=120°，则∠BOD的度数为（ ）
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次不等式-x2+2x+m＞0的解集为 ．
如图，已知△OAB的顶点A、B分别在反比例函数y=
（x>0）
已知：如图，在平面直角坐标系中，抛物线y=ax2+x的对称轴为直线x=2，顶点为A．点P为抛物线对称轴上一点，连接OA、OP．当OA⊥OP时，P点坐标为 ．
+2
如图，在△ABC中，∠C=90°，在AC边上找一点O，使得以O为圆心的圆分别与BC、AB相切．（尺规作图，保留作图痕迹，不写作法）
如图，点C，F在线段BD上，AB∥DE，
=