德优网2021陕西省西安市碑林区西工大附中初中数学模考模拟
2021年陕西省西安市西工大附中中考数学五模试卷
试卷总分:120分
命题人:dcyx2021
考试时长:120分钟
一、选择题(10小题共30分)
1.
(本题3分)
数轴上,把表示2的点向左平移3个单位长度得到的点所表示的数是( )
2.
(本题3分)
陕西省创建“国家级森林城市”以来,为改善生态环境,多地实行退耕还林、防沙治沙,为此小华制作了一个正方体,其展开图如图所示,原正方体中与“态”字相对面上的汉字是( )

3.
(本题3分)
下列运算正确的是( )
A.
|
B.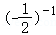 =﹣2 =﹣2
|
|
C.(﹣3m2)3=27m6
|
D.(a﹣1)2=a2﹣1
|
4.
(本题3分)
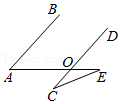
如图,已知AE交CD于点O,AB∥CD,OC=OE,∠A=50°,则∠C的大小为( )
5.
(本题3分)
若一个正比例函数的图象经过A(m,6),B(5,n)两点,则m,n一定满足的关系式为( )
A.m+n=11
B.m﹣n=1
C.mn=30
D.
6.
(本题3分)
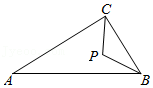
如图,Rt△ABC中,∠ACB=90°,∠A=30°,BP平分∠ABC,BP=CP=2,则AB的长为( )
A.4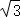
B.6
C.4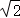
D.4
7.
(本题3分)
在同一坐标系中,若直线y=﹣x+b与直线y=kx﹣4的交点在第一象限,则下列关于k、b的判断正确的是( )
A.k<0,b<0
B.k<0,b>0
C.k>0,b<0
D.k>0,b>0
8.
(本题3分)
如图,矩形ABCD中,AD=3,AB=4,过点A、C分别作相距为3的平行线段AE、CF,分别交CD、AB于点E、F,则tan∠DAE的值是( )

9.
(本题3分)
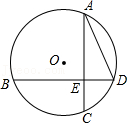
如图,⊙O的弦AC=BD,且AC⊥BD于E,连接AD,若AD=3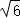 ,则⊙O的周长为( )
,则⊙O的周长为( )
10.
(本题3分)
抛物线y=ax2+bx+c(a>0)过点(1,0)和点(0,﹣3),且顶点在第三象限,设n=a﹣b+c,则n的取值范围是( )
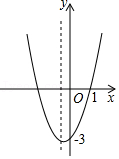
A.﹣3<n<﹣1
B.﹣3<n<0
C.﹣6<n<﹣3
D.﹣6<n<0
二、填空题(4小题共12分)
11.
(本题3分)
比较大小:﹣3_______﹣2 (填“>”、“<”或“=”).
(填“>”、“<”或“=”).
12.
(本题3分)
已知正六边形的周长为12,则这个正六边形的边心距是_______.
13.
(本题3分)
如图,反比例函数y= 的图象上有A、B两点,过点B作BD⊥y轴于点D,交
的图象上有A、B两点,过点B作BD⊥y轴于点D,交
OA于点C.若AC=2OC,△BOC的面积为2,则k的值为_______.

14.
(本题3分)
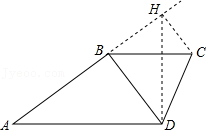
如图,在四边形ABCD中,AD=6,∠C=60°,连接BD,BD⊥AB且BD=CD,求四边形ABCD面积的最大值.小明过点C作CH⊥AB,交AB的延长线于点H,连接DH,则∠AHD的正弦值为_________,据此可得四边形ABCD的面积最大值为_________.
三、解答题(11小题共78分)
15.
(本题5分)
计算: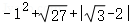 ﹣(π﹣3.14)0.
﹣(π﹣3.14)0.
16.
(本题5分)
化简:[(3x﹣y)(3x+y)﹣2xy﹣2(2x+y)(2x﹣y)]÷(x﹣y).
17.
(本题5分)
尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)

18.
(本题5分)
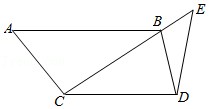
如图,AB∥CD,点E在CB的延长线上,连接BD,∠A=∠E,AC=ED.求证:∠CBD=∠CDB.
19.
(本题7分)
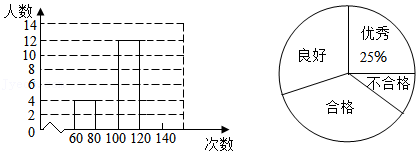
促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,一分钟跳绳次数记作x,共分为四个等级,60≤x<80记为不合格,80≤x<100记为合格,100≤x<120记为良好,120≤x<140记为优秀,并根据调查统计结果绘制了统计图:
请结合上述信息完成下列问题:
(1)请补全频数分布直方图,扇形统计图中“良好”等级对应的圆心角的度数是____;
(2)该组数据的中位数落在_______(填等级);
(3)根据抽样调查结果,请估计该校学生一分钟跳绳次数的平均数.
20.
(本题7分)
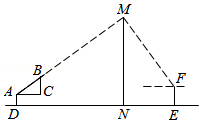
建筑工地的塔吊示意如图,爱钻研和思考问题的小亮和小颖来到塔吊前,测量塔吊的高度.小亮拿出自制的直角三角形ABC,将Rt△ABC的直角边AC平行于地面,眼睛通过斜边AB观察,一边观察一边走动,使得A、B、M共线,已知AB=0.5m,BC=0.3m,此时,小颖测量小亮距塔吊的距离DN=40米,AD=1米.随后,小颖站在另一侧的点E处,观察塔吊的顶部M的仰角是60°,经过测量EF=1.5米,那么根据以上数据你能求出小颖与塔吊的距离NE的长度吗?(结果保留根号)
21.
(本题7分)
九年级某班要召开一次“走近抗疫英雄,讲好中国故事”主题班会活动,李老师制作了编号为A、B、C、D的4张卡片(如图,除编号和内容外,其余完全相同),并将它们背面朝上洗匀后放在桌面上.
(1)小明随机抽取1张卡片,抽到卡片编号为B的概率为______;
(2)小明从4张卡片中随机抽取1张(不放回),小丽再从余下的3张卡片中随机抽取1张,然后根据抽取的卡片讲述相关英雄的故事,求小明、小丽两人中恰好有一人讲述钟南山抗疫故事的概率(请用“画树状图”或“列表”等方法写出分析过程).

23.
(本题8分)
如图,在△ABC中,AB=AC,AE平分∠BAC,∠ABC的平分线BM
交AE于点M,点O在AB上,以点O为圆心,OB长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证:AE为⊙O的切线.
(2)若BC=8,AC=12时,求BM的长.

24.
(本题9分)
在平面直角坐标系中,经过点(1,﹣10),(2,﹣12)的抛物线y=ax2+bx﹣6与x轴交于A、B两点(A点在B点的左侧),与y轴交于点C.
(1)求此抛物线的函数表达式;
(2)在抛物线确定一点P,使∠ACP=90°,求点P的坐标;
(3)是否在x轴上存在点M,使∠OCM+∠ACO=45°,若存在,求出点M的坐标;若不存在,请说明理由.

25.
(本题12分)
问题提出
(1)如图①,在Rt△ABC中,∠ACB=90°,AC=BC.过点C作直线l,再分别过点A、B作AM⊥l于M,BN⊥l于N.则线段MN、AM、BN之间的数量关系为___________;
(2)如图②,在Rt△ABC中,∠C=90°,AC=30,BC=40,点P在AB上,点E、F分别是边AC、BC上,且∠ABC=∠FPB,PE⊥PF.设BP=x,求四边形CEPF的面积y与x之间的函数关系式;
(3)如图③是一个圆形广场,其中四边形ACBD规划为园林绿化区(四个顶点均在圆上),且要求∠ACB=90°,AC=30米,BC=40米,连接AB、CD交于点P.为了更好的美化环境,需要在AC、BC边上分别确定点E、F,且满足∠ABC=∠FPB,PE⊥PF.为了整体布局,计划在四边形CEPF内种植花卉,在四边形ACBD剩余区域种植草坪.已知花卉每平方米的价格是60元,草坪每平方米的价格是90元,从实用角度希望四边形CEPF的面积最大.根据设计要求,求出当四边形CEPF的面积最大时种植花卉和草坪的总费用.

转载声明:
本试卷内容属于发布者收集录入,如涉及版权请告知发布者本人!


![]()
![]()
![]()
![]()








