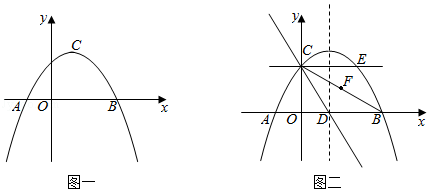二次函数压轴题型采集卷

1. （本题0分）已知抛物线y＝ax²﹣2ax﹣3+2a²（a≠0）．
（1）求这条抛物线的对称轴；
（2）若该抛物线的顶点在x轴上，求其解析式；
（3）设点P（m，y₁），Q（3，y₂）在抛物线上，若y₁＜y₂，求m的取值范围．

解析

纠错

下载

相似

组卷

2. （本题0分）已知抛物线y＝a（x﹣3）²+2经过点（1，﹣2）．
（1）求a的值；
（2）若点A（m，y₁）、B（n，y₂）（m＜n＜3）都在该抛物线上，试比较y₁与y₂的大小．

解析

纠错

下载

相似

组卷

3. （本题0分）在平面直角坐标系xOy中，M（x₁，y₁），N（x₂，y₂）为抛物线y＝ax²+bx+c（a＞0）上任意两点，其中x₁＜x₂．
（1）若抛物线的对称轴为x＝1，当x₁，x₂为何值时，y₁＝y₂＝c；
（2）设抛物线的对称轴为x＝t，若对于x₁+x₂＞3，都有y₁＜y₂，求t的取值范围．

解析

纠错

下载

相似

组卷

4. （本题0分）在平面直角坐标系xOy中，抛物线y＝x²﹣4x+3与x轴交于点A、B（点A在点B的左侧），与y轴交于点C．
（1）求直线BC的表达式；
（2）垂直于y轴的直线l与抛物线交于点P（x₁，y₁），Q（x₂，y₂），与直线BC交于点N（x₃，y₃），若x₁＜x₂＜x₃，结合函数的图象，求x₁+x₂+x₃的取值范围．

解析

纠错

下载

相似

组卷

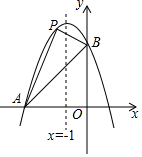
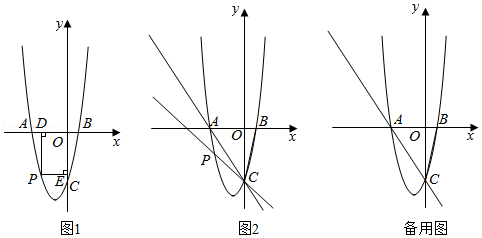
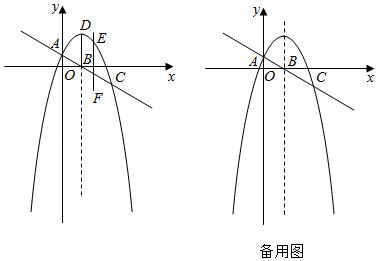
5. （本题0分）如图一，抛物线y＝ax²+bx+c过A（﹣1，0）、B（3，0）、C（0，

）三点．

（1）求该抛物线的解析式；
（2）P（x₁，y₁）、Q（4，y₂）两点均在该抛物线上，若y₁≥y₂，求P点横坐标x₁的取值范围；
（3）如图二，过点C作x轴的平行线交抛物线于点E，该抛物线的对称轴与x轴交于点D，连结CD、CB，点F为线段CB的中点，点M、N分别为直线CD和CE上的动点，求△FMN周长的最小值．

解析

纠错

下载

相似

组卷

6. （本题0分）已知关于x的一元二次方程mx²+（1﹣5m）x﹣5＝0（m≠0）．
（1）求证：无论m为任何非零实数，此方程总有两个实数根；
（2）若抛物线y＝mx²+（1﹣5m）x﹣5与x轴交于A（x₁，0）、B（x₂，0）两点，且|x₁﹣x₂|＝6，求m的值；
（3）若m＞0，点P（a，b）与Q（a+n，b）在（2）中的抛物线上（点P、Q不重合），求代数式4a²﹣n²+8n的值．

解析

纠错

下载

相似

组卷

7. （本题0分）如图，一元二次方程x²+2x﹣3＝0的二根x₁，x₂（x₁＜x₂）是抛物线y＝ax²+bx+c与x轴的两个交点B，C的横坐标，且此抛物线过点A（3，6）．
（1）求此二次函数的解析式；
（2）写出不等式ax²+bx+c≥0的解集；
（3）设此抛物线的顶点为P，对称轴与线段AC相交于点Q，求点P和点Q的坐标；
（4）在x轴上有一动点M，当MQ+MA取得最小值时，求M点的坐标．

解析

纠错

下载

相似

组卷

8. （本题0分）如图，在平面直角坐标系xOy中，已知直线y＝

x﹣2与x轴交于点A，与y轴交于点B，过A、B两点的抛物线y＝ax²+bx+c与x轴交于另一点C（﹣1，0）．
（1）求抛物线的解析式；
（2）在抛物线上是否存在一点P，使S_△PAB＝S_△OAB？若存在，请求出点P的坐标，若不存在，请说明理由；
（3）点M为直线AB下方抛物线上一点，点N为y轴上一点，当△MAB的面积最大时，求MN+

ON的最小值．

解析

纠错

下载

相似

组卷

9. （本题0分）如图，在平面直角坐标系中，已知抛物线y＝ax²+bx﹣5与x轴交于A（﹣1.0）．B（5，0）两点，与y轴交于点C．
（1）求地物线的解析式；
（2）在地物线的对称轴上找一点M．使得MA+MC最小，请求出点M的坐标；
（3）在直线BC下方抛物线上是否存在点P，使得△PBC的面积最大？若存在．请求出点P的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

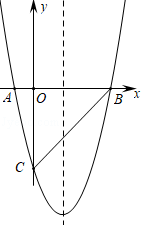
10. （本题0分）如图，已知抛物线经过两点A（﹣3，0），B（0，3），且其对称轴为直线x＝﹣1．
（1）求此抛物线的解析式；
（2）若点P是抛物线上点A与点B之间的动点（不包括点A，点B），求△PAB的面积的最大值，并求出此时点P的坐标．

解析

纠错

下载

相似

组卷

11. （本题0分）如图，在平面直角坐标系xOy中，四边形ABCD是边长为5的菱形，顶点A，C，D均在坐标轴上，sinB＝

．
（1）求过A，C，D三点的抛物线的解析式；
（2）记直线AB的解析式为y₁＝mx+n，（1）中抛物线的解析式为y₂＝ax²+bx+c，求当y₁＞y₂时，自变量x的取值范围；
（3）设直线AB与（1）中抛物线的另一个交点为E，P点为抛物线上A．E两点之间的一个动点，且直线PE交x轴于点F，问：当P点在何处时，△PAE的面积最大？并求出面积的最大值．

解析

纠错

下载

相似

组卷

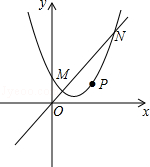
12. （本题0分）如图，抛物线y＝ax²+bx+c（a≠0）与直线y＝kx（k≠0）相交于点M（1，1），N（3，3），且这条抛物线的对称轴为x＝1．
（1）若将该抛物线平移使得其经过原点，且对称轴不变，求平移后的抛物线的表达式及k的值．
（2）设P为直线y＝kx下方的抛物线上一点，求△PMN面积的最大值及此时P点的坐标．

解析

纠错

下载

相似

组卷

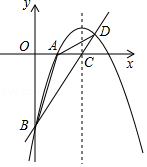
13. （本题0分）如图，已知抛物线y＝ax²+4x+c经过A（2，0）、B（0，﹣6）两点，其对称轴与x轴交于点C．
（1）求该抛物线和直线BC的解析式；
（2）设抛物线与直线BC相交于点D，求△ABD的面积；
（3）在该抛物线的对称轴上是否存在点Q，使得△QAB的周长最小？若存在，求出Q点的坐标及△QAB最小周长；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

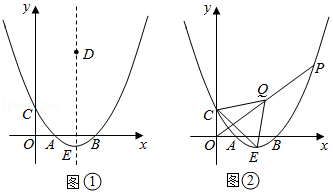
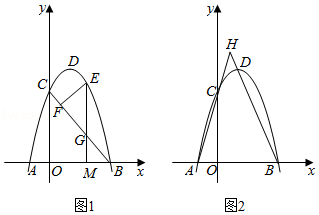
14. （本题0分）二次函数y＝ax²+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．．
（1）求这个二次函数的表达式，并写出点E的坐标；
（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；
（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．

解析

纠错

下载

相似

组卷

15. （本题0分）如图，Rt△AOB的直角边OA在x轴上，OA＝2，AB＝1，将Rt△AOB绕点O逆时针旋转90°得到Rt△COD，抛物线y＝﹣

x²+bx+c经过B、D两点．
（1）求二次函数的解析式；
（2）连接BD，点P是抛物线上一点，直线OP把△BOD的周长分成相等的两部分，求点P的坐标．

解析

纠错

下载

相似

组卷

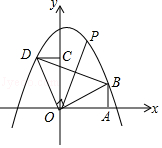
16. （本题0分）如图，抛物线y＝ax²﹣3ax﹣4a的图象经过点C（0，2），交x轴于点A、B（点A在点B左侧），连接BC，直线y＝kx+1（k＞0）与y轴交于点D，与BC上方的抛物线交于点E，与BC交于点F．
（1）求抛物线的解析式及点A、B的坐标；
（2）

是否存在最大值？若存在，请求出其最大值及此时点E的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

17. （本题0分）如图，抛物线y＝﹣

x²+bx+c与x轴交于点A（﹣1，0）和点B（4，0），与y轴交于点C，连接BC，点P是线段BC上的动点（与点B，C不重合），连接AP并延长AP交抛物线于点Q，连接CQ，BQ，设点Q的横坐标为m．
（1）求抛物线的解析式和点C的坐标；
（2）当△BCQ的面积等于2时，求m的值；
（3）在点P运动过程中，

是否存在最大值？若存在，求出最大值；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

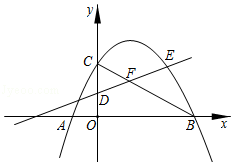
18. （本题0分）在平面直角坐标系中，抛物线y＝ax²+bx﹣3过点A（﹣3，0），B（1，0），与y轴交于点C，顶点为点D．
（1）求抛物线的解析式；
（2）点P为直线CD上的一个动点，连接BC；
①如图1，是否存在点P，使∠PBC＝∠BCO？若存在，求出所有满足条件的点P的坐标；若不存在，请说明理由；
②如图2，点P在x轴上方，连接PA交抛物线于点N，∠PAB＝∠BCO，点M在第三象限抛物线上，连接MN，当∠ANM＝45°时，请直接写出点M的坐标．

解析

纠错

下载

相似

组卷

19. （本题0分）如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax²+bx+

（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．
（1）求这条抛物线对应的函数表达式；
（2）已知R是抛物线上的点，使得△ADR的面积是▱OABC的面积的

，求点R的坐标；
（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE＝45°，求点P的坐标．

解析

纠错

下载

相似

组卷

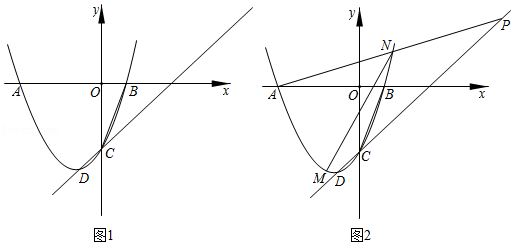
20. （本题0分）抛物线y＝x²+bx+c经过点A（﹣3，0）和点B（2，0），与y轴交于点C．
（1）求该抛物线的函数表达式；
（2）点P是该抛物线上的动点，且位于y轴的左侧．
①如图1，过点P作PD⊥x轴于点D，作PE⊥y轴于点E，当PD＝2PE时，求PE的长；
②如图2，该抛物线上是否存在点P，使得∠ACP＝∠OCB？若存在，请求出所有点P的坐标：若不存在，请说明理由．

解析

纠错

下载

相似

组卷

21. （本题0分）如图1，抛物线y＝x²+bx+c交x轴于A，B两点，其中点A的坐标为（1，0），与y轴交于点C（0，﹣3）．
（1）求抛物线的函数解析式；
（2）点D为y轴上一点，如果直线BD与直线BC的夹角为15°，求线段CD的长度；
（3）如图2，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO，求点P的坐标．

解析

纠错

下载

相似

组卷

22. （本题0分）已知抛物线y＝ax²﹣2ax+c过点A（﹣1，0）和C（0，3），与x轴交于另一点B，顶点为D．
（1）求抛物线的解析式，并写出D点的坐标；
（2）如图1，E为线段BC上方的抛物线上一点，EF⊥BC，垂足为F，EM⊥x轴，垂足为M，交BC于点G．当BG＝CF时，求△EFG的面积；
（3）如图2，AC与BD的延长线交于点H，在x轴上方的抛物线上是否存在点P，使∠OPB＝∠AHB？若存在，求出点P的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

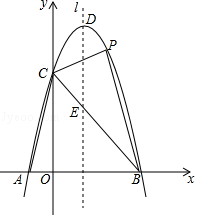
23. （本题0分）如图，抛物线y＝x²+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．
（1）求该抛物线的表达式；
（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．

解析

纠错

下载

相似

组卷

24. （本题0分）如图，抛物线y＝ax²+bx+8（a≠0）与x轴交于点A（﹣2，0）和点B（8，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E．
（1）求抛物线的表达式；
（2）点P是第一象限内抛物线上的动点，连接PB，PC，当S_△PBC＝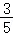

S_△ABC时，求点P的坐标；
（3）点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M，使得以点M，N，E为顶点的三角形与△OBC相似？若存在，求点M的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

25. （本题0分）已知二次函数y＝ax²+2x+c（a≠0）的图象与x轴交于A、B（1，0）两点，与y轴交于点C（0，﹣3），
（1）求二次函数的表达式及A点坐标；
（2）D是二次函数图象上位于第三象限内的点，求点D到直线AC的距离取得最大值时点D的坐标；
（3）M是二次函数图象对称轴上的点，在二次函数图象上是否存在点N，使以M、N、B、O为顶点的四边形是平行四边形？若有，请写出点N的坐标（不写求解过程）．

解析

纠错

下载

相似

组卷

26. （本题0分）如图，抛物线过点A（0，1）和C，顶点为D，直线AC与抛物线的对称轴BD的交点为B（

，0），平行于y轴的直线EF与抛物线交于点E，与直线AC交于点F，点F的横坐标为

，四边形BDEF为平行四边形．
（1）求点F的坐标及抛物线的解析式；
（2）若点P为抛物线上的动点，且在直线AC上方，当△PAB面积最大时，求点P的坐标及△PAB面积的最大值；
（3）在抛物线的对称轴上取一点Q，同时在抛物线上取一点R，使以AC为一边且以A，C，Q，R为顶点的四边形为平行四边形，求点Q和点R的坐标．

解析

纠错

下载

相似

组卷

27. （本题0分）如图，在平面直角坐标系中，抛物线y＝ax²+bx+2（a≠0）与y轴交于点C，与x轴交于A，B两点（点A在点B的左侧），且A点坐标为（﹣

，0），直线BC的解析式为y＝﹣

x+2．
（1）求抛物线的解析式；
（2）过点A作AD∥BC，交抛物线于点D，点E为直线BC上方抛物线上一动点，连接CE，EB，BD，DC．求四边形BECD面积的最大值及相应点E的坐标；
（3）将抛物线y＝ax²+bx+2（a≠0）向左平移

个单位，已知点M为抛物线y＝ax²+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

28. （本题0分）如图，在平面直角坐标系中，已知抛物线y＝x²+bx+c与直线AB相交于A，B两点，其中A（﹣3，﹣4），B（0，﹣1）．
（1）求该抛物线的函数表达式；
（2）点P为直线AB下方抛物线上的任意一点，连接PA，PB，求△PAB面积的最大值；
（3）将该抛物线向右平移2个单位长度得到抛物线y＝a₁x²+b₁x+c₁（a₁≠0），平移后的抛物线与原抛物线相交于点C，点D为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点E，使以点B，C，D，E为顶点的四边形为菱形，若存在，请直接写出点E的坐标；若不存在，请说明理由．

解析

纠错

下载

相似

组卷

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

普通登录

手机登录

微信扫码立即登录

二次函数压轴题型采集卷