服务热线
，0），直线BC的解析式为y＝﹣
x+2．
个单位，已知点M为抛物线y＝ax2+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．
x+2，令y＝0，则x＝3
，令x＝0，则y＝2，
，0）、（0，2）；
）（x﹣3
）＝a（x2﹣2
x﹣6）＝ax2﹣2
a﹣6a，
，
x2+
x+2①；
（x+
）②，
，故点D（4
，﹣
），
x+2，
时，yCD＝﹣
x+2＝﹣2，即点H（3
，﹣2），
x2+
x+2），则点F（x，﹣
x+2），
×EF×OB+
×（xD﹣xC）×BH＝
×（﹣
x2+
x+2+
x﹣2）×3
+
×4
×2＝﹣
x2+3x+4
，
＜0，故S有最大值，当x＝
时，S的最大值为
，此时点E（
，
）；
x2+
x+2＝﹣
（x
）2+
，抛物线y＝ax2+bx+2（a≠0）向左平移
个单位，
x2+
，
，0）、（
，
）；设点M（
，m），点N（n，s），s＝﹣
n2+
；
个单位向上平移
个单位得到E，同样点M（N）向右平移
个单位向上平移
个单位得到N（M），
±
＝n，
n2+
＝﹣
或
，
，﹣
）或（﹣
，
）；
+
＝n+
，解得：n＝﹣
，
n2+
＝
＝
，
，
）；
，﹣
）或（﹣
，
）或（﹣
，
）．
，0），平行于y轴的直线EF与抛物线交于点E，与直线AC交于点F，点F的横坐标为
，四边形BDEF为平行四边形．
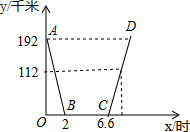早晨小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图是小明出行的过程中，他距西安的距离（千米）与他离家的时间（时）之间的关系图象．| 鲢鱼 | 草鱼 | 青鱼 | |
| 每辆汽车载鱼量（吨） | 8 | 6 | 5 |
| 每吨鱼获利（万元） | 0.25 | 0.3 | 0.2 |
亦世凡华
2021-01-06
初中数学 | 解答题
纠错
收藏
下载
相似
组卷
解析
