服务热线
搜题▪组卷
，
，
时，y＝4，
，
，
．
．
．
．
，
，
；
，
，
．
，把（﹣1，0）代入，得b＝
，
，联立得
，
，
，
＝
，
，
．
或n＝3（舍去）．
，
．
排球运动是一种全身性的体育活动，它能够有效提升心肺功能，改善柔韧性和协调性．一名排球运动员在原点O处训练发球，球网MN高2.4m,与原点O的水平距离OM为9m,且MN与地面垂直，球场的边界（点K）与原点O的水平距离为18m,排球（看作点）从点O的正上方点P（0，2）处发出，排球经过的路径可以看作抛物线的一部分，当排球在距离发出点水平距离6m时，与地面的垂直距离最大，为3m,落地点为点H，如图，以点O为原点，点O，M，H，K所在的直线为x轴，OP所在直线为y轴，建立平面直角坐标系．（图中所有的点均在同一平面内）．
如图，隧道的截面由抛物线和长方形构成，长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
，当水平距离为4m时，实心球行进至最高点3m处．
米，则点E与隧道左壁OC之间的距离为多少米？
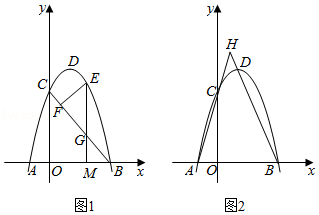
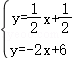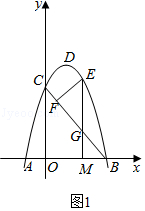
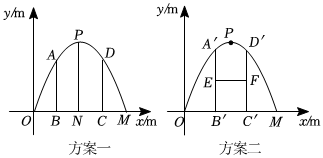
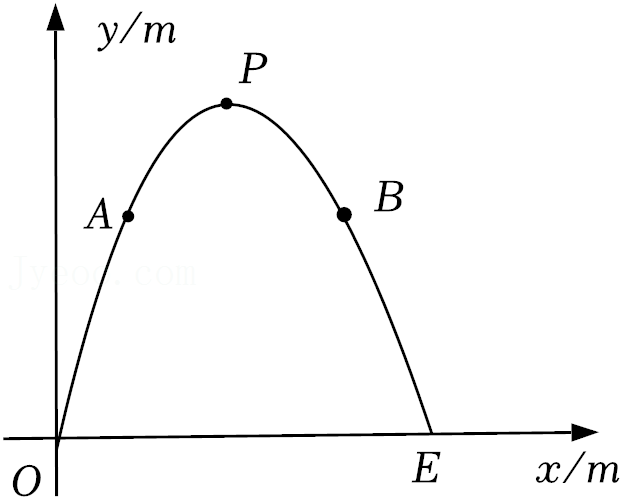
| 飞行水平距离x/m | 0 | 20 | 30 | 50 | 80 | … |
| 飞行高度y/m | 0 | 40 | 54 | 70 | 64 | … |
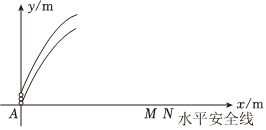
亦世凡华
2021-01-06
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
