德优网2021陕西省西安市交大附中初中数学考试期中七年级下
2020-2021学年陕西省西安市交大附中七下数学期中试卷
试卷总分:100分
命题人:dcyx2021
考试时长:120分钟
1.
（3分）
下列运算正确的是（ ）
A.a2•a4=a8
B.（-2a）3=-6a3
C.m3÷（-m）2=m
D.a4+a4=a8
2.
（3分）
截至4月2日，全球累计确诊新冠肺炎病例约1.3亿例．我们切不可掉以轻心，要做好日常防护．科学研究表明，导致新冠肺炎的新冠病毒比细菌小很多，平均直径仅为0.000000098m．这个数用科学记数法表示为（ ）
A.0.98×10-7
B.9.8×10-8
C.98×10-8
D.9.8×10-9
3.
（3分）
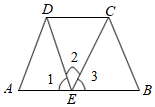如图所示，下列推理不正确的是（ ）
A.若∠1=∠B，则BC∥DE
B.若∠2=∠ADE，则AD∥CE
C.若∠A+∠ADC=180°，则AB∥CD
D.若∠B+∠BCD=180°，则BC∥DE
4.
（3分）
下列各式能用平方差公式计算的是（ ）
A.（2a+b）（a-2b）
B.（a-2b）（2b-a）
C.（2a-b）（-2a+b）
D.（b-2a）（-2a-b）
5.
（3分）
下面说法：①三角形的三条高交于同一点；②面积相等的两个正方形全等；③两条射线不相交就平行；④同位角相等．其中正确的有（ ）
6.
（3分）
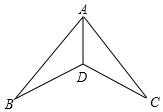如图，下列推理不能求证△ABD≌△ACD的是（ ）
A.DB=DC，AB=AC
B.∠ADC=∠ADB，DB=DC
C.∠C=∠B，∠ADC=∠ADB
D.∠C=∠B，DB=DC
7.
（3分）
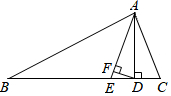
如图，AD，AE为△ABC的高线，角平分线，DF⊥AE于点F．当∠DAC=21°，∠B=25°时，∠DAF的度数为（ ）
8.
（3分）
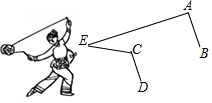
乐乐观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB∥CD，∠BAE=94°，∠DCE=115°，则∠E的度数是（ ）
9.
（3分）
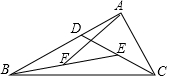
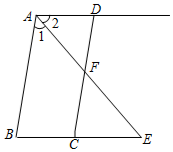
如图，△ABF的面积是2，D是AB边上任意一点，E是CD中点，F是BE中点，△ABC的面积是（ ）
10.
（3分）
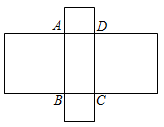
如图，长方形ABCD的两边之差为4，以长方形的四条边分别为边向外作四个正方形，且这四个正方形的面积和为80，则长方形ABCD的面积是（ ）
11.
（3分）
若一个角的补角是43°，则这个角的度数为 ．
12.
（3分）
已知三角形的两边长分别为2和7，第三边为奇数，则它第三边的长是 ．
13.
（3分）
如果2021a=5，2021b=3．那么20212a-3b= ．
14.
（3分）
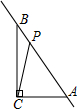
如图，△ABC中，∠ACB=90°，AC=5，BC=12，AB=13，P为直线AB上一动点，连接PC，则线段PC的最小值是 ．
15.
（3分）
当x=-1时，ax2+bx+1的值为-3，则（a-b+2）（3-2a+2b）的值为 ．
16.
（3分）
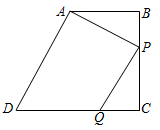
已知：如图，在四边形ABCD中，AB∥CD，∠B=90°，AB=6厘米，BC=8厘米，CD=10厘米，点P从点B出发，以2厘米/秒的速度沿BC向点C运动，同时点Q从点D出发，沿DC向点C运动，连接AP，PQ．则点Q的运动速度为 厘米/秒时，△ABP与△CPQ全等．
17.
（12分）
计算：
（1）（-1）2021-（-2）-2+（3-π）0；
（2）a3a4a+（a2）4-（-2a4）2；
（3）[（a-b）（2a-b）-（a+b）2]÷（-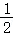
a）．
18.
（6分）
在△ABC中，∠C＞∠B、请用尺规作图法，在AB上找一点P，使∠PCB=∠B．（保留作图痕迹，不写作法．）
19.
（6分）
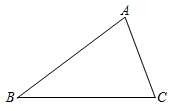
已知：如图，AD∥BC，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E，那么∠B与∠DCE相等吗？试说明理由．请将下面的推理过程补充完整．
解：∠B=∠DCE，理由如下：
∵AE平分∠BAD（已知），
∴∠1=∠2（角平分线定义），
∵AD∥BC（已知），
∴∠2=∠E（ ），
∴∠1=∠E（ ），
又∵∠CFE=∠E（已知），
∴∠CFE=∠ （等量代换），
∴ ∥ （ ），
∴∠B=∠DCE．
20.
（8分）
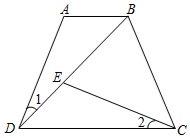
如图，在四边形ABCD中，AB∥CD，∠1=∠2，AD=EC．
（1）求证：△ABD≌△EDC；
（2）若AB=2，BE=3，求CD的长．
21.
（8分）
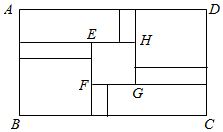
为迎接十四运，某小区修建一个长为（3a-b）米，宽为（a+2b）米的长方形休闲场所ABCD．长方形内筑一个正方形活动区EFGH和连接活动区到矩形四边的四条笔直小路（如图），正方形活动区的边长为（a-b）米，小路的宽均为2米．活动区与小路铺设鹅卵石，其它地方铺设草坪．
（1）求铺设草坪的面积是多少平方米；
（2）当a=10，b=4时，需要铺设草坪的面积是多少？
22.
（12分）
问题背景：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=4，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，则得到△ADC≌△EDB，小明证明△BED≌△CAD用到的判定定理是： （用字母表示）；
问题解决：小明发现：解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．请写出小明解决问题的完整过程；
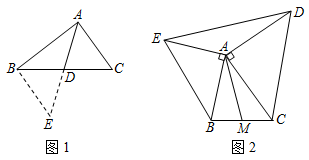
拓展应用：以△ABC的边AB，AC为边向外作△ABE和△ACD，AB=AE，AC=AD，∠BAE=∠CAD=90°，M是BC中点，连接AM，DE．当AM=3时，求DE的长．
解析
收藏
下载
相似
组卷