如图，在△ACB中，&ang;ACB=90&deg;，CD是△ACB的高，垂足为点D．br /> （1）求证：&ang;BCD=&ang;CAD；br /> （2）若点F是△ABC的边BC上一点，连接AF交CD于点E，且&ang;CEF=&ang;CFE．求证：AF平分&ang;CAB．br /> img alt="德优题库" src="/math/image/20

首页 > 试题列表 > 单题解析

24124. （2018•汇知中学•八下期中）如图，在△ACB中，∠ACB=90°，CD是△ACB的高，垂足为点D．
（1）求证：∠BCD=∠CAD；
（2）若点F是△ABC的边BC上一点，连接AF交CD于点E，且∠CEF=∠CFE．求证：AF平分∠CAB．
$德优题库$

共享时间:2018-05-26 难度:4

纠错

下载

相似

组卷

[考点]

三角形内角和定理三角形的外角性质

[答案]

见试题解答内容

[解析]

（1）证明：∵CD是△ACB的高，
∴∠ADC=90°，
∴∠CAD+∠ACD=90°，
∵∠ACB=90°，
∴∠ACD+∠BCD=90°，
∴BCD=∠CAD．

（2）证明：∵∠ADC=∠CDB=90°，
∴∠ACD+∠DCB=90°，∠DCB+∠B=90°，
∴∠ACD=∠B，
∵∠CEF=∠EAC+∠ACE，∠CFE=∠BAF+∠B，∠CEF=∠CFE，
∴∠CAE=∠BAE，
∴AF平分∠CAB．

[点评]

本题考查了"三角形内角和定理,三角形的外角性质"，属于"必考题"，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．

转载声明：

本题解析属于发布者收集录入，如涉及版权请告知发布者本人！

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

20154. （2021•西工大附中•四模）如图所示，点E在△ABC外部，点D在BC边上，DE交AC于F，若∠1＝∠2＝∠3，AD＝AB，求证：AC＝AE．

共享时间:2021-05-31 难度:3 相似度:1

解析

纠错

下载

组卷

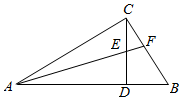
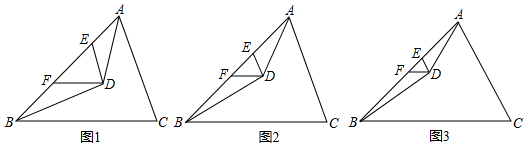
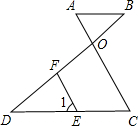24173. （2019•爱知中学•七下期中） $德优题库$ 已知，如图，AC和BD交于点O，E是CD上一点，F是OD上点，FE∥OC，∠1=∠A．
（1）试判断AB和CD的位置关系，并说明理由．
（2）若∠B=30°，∠1=65°，求∠DOC的度数．

共享时间:2019-05-05 难度:3 相似度:1

解析

纠错

下载

组卷

25753. （2023•西工大附中•六模）中国古代在公元前2世纪就制成了世界上最早的潜望镜，西汉初年成书的《淮南万毕术》中有这样的记载：“取大镜高悬，悬水盆于其下，则见四邻矣”，如图1所示，其工作方法主要利用了光的反射原理，在图2中，AB呈水平状态，入射角∠BOC=30°，∠OAD=15°（入射角等于反射角，OC、AD为法线），若AB=10

米，求光线从O到达A经过的距离（即OA的长度）．
$德优题库$

共享时间:2024-03-12 难度:3 相似度:1

解析

纠错

下载

组卷

1138. （2020•陕西省•副题）如图，在△ABC中，AB=AC，D是BA延长线上一点，E是AC的中点，连接DE并延长，交BC于点M，∠DAC的平分线交DM于点F．求证：AF=CM．
$德优题库$

共享时间:2020-07-31 难度:3 相似度:0.83

解析

纠错

下载

组卷

23419. （2020•西工大附中•八上二月）已知：如图，在Rt△ABC中，∠C=90°，点D在CB边上，∠DAB=∠B，点E在AB边上且满足∠CAB=∠BDE．
求证：AE=BE．
$德优题库$

共享时间:2021-01-09 难度:3 相似度:0.83

解析

纠错

下载

组卷

23812. （2021•益新中学•五模）如图，在平行四边形ABCD中，E是BC上一点，点F在线段DE上，DE=AD，且∠AFE=∠ADC，求证：DF=EC．
$德优题库$

共享时间:2021-06-18 难度:3 相似度:0.83

解析

纠错

下载

组卷

24152. （2021•高新一中•七下期中）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分∠AEF交CD于点M，且∠FEM=∠FME．
（1）猜想直线AB与直线CD有怎样的位置关系？说明你的理由；
（2）若点G为直线CD上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN=α，∠EGF=β．
①如图2，当点G在射线FD上运动时，若β=56°，求α的度数；
②当点G在直线CD上运动时，请直接写出α和β的数量关系．
$德优题库$

共享时间:2021-04-29 难度:5 相似度:0.83

解析

纠错

下载

组卷

24175. （2019•爱知中学•七下期中）（1）如图1，在△ABC中，AD，BD分别平分∠BAC和∠ABC，AD、BD相交于点D．过点D作DE∥AC，DF∥BC分别交AB于点E、F．
①若∠EDF=80°，则∠ADB= ．
②若∠C=x°，则∠ADB= ．
（2）如图2，在△ABC中，若∠BAD=

∠BAC，∠ABD=

∠ABC，AD，BD相交于点D．过点D作DE∥AC，DF∥BC分别交AB于点E、F．若∠EDF=60°．则∠ADB= ．
（3）如图3，在△ABC中，AD、BD分别平分∠BAC、∠ABC的n等分线，AD、BD相交于点D．若∠BAD=

∠BAC，∠ABD=

∠ABC．过点D作DE∥AC．DF∥BC分别交AB于点E、F．若∠EDF=x°，则∠ADB的度数是多少？（用x，n表示）
$德优题库$

共享时间:2019-05-05 难度:4 相似度:0.83

解析

纠错

下载

组卷

25991. （2024•铁一中学•三模）如图，在△ABC中，∠BAC=90°，∠ABC=30°，请用尺规作图法在边CB上求作一点D，使得AD将△ABC分为两个等腰三角形．（保留作图痕迹，不写作法）
$德优题库$

共享时间:2024-03-12 难度:2 相似度:0.83

解析

纠错

下载

组卷

25993. （2024•高新一中•六模） $德优题库$ 如图，四边形ABCD中，∠B=90°，AC是对角线，∠ACB=50°，请用尺规作图法，在CD边上求作一点P，使∠CPB=40°．（不写作法，保留作图痕迹）

共享时间:2024-03-12 难度:3 相似度:0.83

解析

纠错

下载

组卷

6214. （2017•漳州双语实验学校•一模）如图，△ABC中，∠A=2∠B，CD平分∠ACB交AB于点D．点E在边BC上，且ED=EB．求证：CE=CA．
$德优题库$

共享时间:2017-02-28 难度:3 相似度:0.75

解析

纠错

下载

组卷

24200. （2017•南靖县星光中学并入船中•八下期中）阅读下列材料：
小华遇到这样一个问题，如图1，△ABC中，∠ACB=30°，BC=6，AC=5，在△ABC内部有一点P，连接PA、PB、PC，求PA+PB+PC的最小值．
小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线段最短”，就可以求出这三条线段和的最小值了．他先后尝试了翻折、旋转、平移的方法，发现通过旋转可以解决这个问题．他的做法是，如图2，将△APC绕点C顺时针旋转60°，得到△EDC，连接PD、BE，则BE的长即为所求．
（1）请你写出图2中，PA+PB+PC的最小值为；
（2）参考小华的思考问题的方法，解决下列问题：
①如图3，菱形ABCD中，∠ABC=60°，在菱形ABCD内部有一点P，请在图3中画出并指明长度等于PA+PB+PC最小值的线段（保留画图痕迹，画出一条即可）；②若①中菱形ABCD的边长为4，请直接写出当PA+PB+PC值最小时PB的长．
$德优题库$

共享时间:2017-05-06 难度:5 相似度:0.64

解析

纠错

下载

组卷

dyhz2022

2018-05-26

初中数学 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2017-2018学年陕西省西安市汇知中学八下数学期中试卷

更新:2018-05-26 02:40浏览量:619

普通登录

手机登录

微信扫码立即登录