某次数学活动时，数学兴趣小组成员小明研究函数y=-img height="35" src="/uploads/meth/20211203/aae10c87ccc6eebf95c9953d4cb8ac94.png" width="13" />（x-2）sup>2/sup>+|x-2|+3的图象和性质．br /> （1）如表是该函数y与自变量x的几组对应值： table class=

首页 > 试题列表 > 单题解析

23089. （2021•高新一中•九上期中）某次数学活动时，数学兴趣小组成员小明研究函数y=-

（x-2）²+|x-2|+3的图象和性质．
（1）如表是该函数y与自变量x的几组对应值：

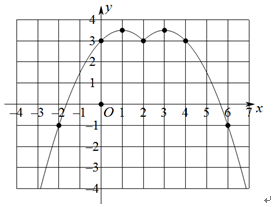
x	…	-2	0	1	2	3	4	6	…
y	…	-1	m	3.5	3	n	3	-1	…

其中，m的值为        ，n的值为        ；
（2）如图，在平面直角坐标系xOy中，描出表中各组对应值为坐标的点，再根据描出的点，画出该函数图象；
（3）根据函数图象回答下列问题；
①该图象的对称轴为：       ；
②该函数的增减性为：当        时，y随x的增大而增大，当        时，y随x的增大而减少；
③该函数的最值为：当x=       时，函数取得最大值，且最大值为        ．
$德优题库$

共享时间:2021-11-25 难度:4

纠错

下载

相似

组卷

[考点]

二次函数的图像二次函数的性质二次函数的顶点坐标二次函数图像的最值问题

[答案]

（1）3，3.5；
（2）见解析；
（3）x＜1或2＜x＜3，x＞3或1＜x＜2，1或3，3.5．

[解析]

解：（1）当x=0时，y=-2+2+3=3，即m=3，
当x=3时，y=-0.5+1+3=3.5，即n=3.5
故答案为：3，3.5；
（2）图象如图所示：
菁优网

（3）①图象关于直线x=2对称；
②当x＜1或2＜x＜3时，y随x的增大而增大；
当x＞3或1＜x＜2时，y随x的增大而减小；
③当x=1或3时，函数取得最大值，且最大值为3.5；
故答案为：x＜1或2＜x＜3，x＞3或1＜x＜2，1或3，3.5．

[点评]

本题考查了"二次函数的图像,二次函数的性质,二次函数的顶点坐标,二次函数图像的最值问题"，属于"综合题"，熟悉考点和题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请告知发布者本人！

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

25627. （2023•爱知中学•二模）如图1所示是一座古桥，桥拱截面为抛物线，如图2，AO，BC是桥墩，桥的跨径AB为20m,此时水位在OC处，桥拱最高点P离水面6m,在水面以上的桥墩AO，BC都为2m.以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系，其中x（m）是桥拱截面上一点距桥墩AO的水平距离，y（m）是桥拱截面上一点距水面OC的距离．
$德优题库$
（1）求此桥拱截面所在抛物线的表达式；
（2）有一艘游船，其左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在河中航行．当水位上涨2m时，水面到棚顶的高度为3m,遮阳棚宽12m,问此船能否通过桥洞？请说明理由．

共享时间:2023-04-28 难度:2 相似度:1.5

解析

纠错

下载

组卷

23085. （2021•高新一中•九上期中）求下列二次函数图象的对称轴和顶点坐标：
（1）y=x²-4x-1；
（2）y=-2x²-5x+7．

共享时间:2021-11-25 难度:3 相似度:1.5

解析

纠错

下载

组卷

61. （2020•北京市•真题）在平面直角坐标系xOy中，M（x₁，y₁），N（x₂，y₂）为抛物线y＝ax²+bx+c（a＞0）上任意两点，其中x₁＜x₂．
（1）若抛物线的对称轴为x＝1，当x₁，x₂为何值时，y₁＝y₂＝c；
（2）设抛物线的对称轴为x＝t，若对于x₁+x₂＞3，都有y₁＜y₂，求t的取值范围．

共享时间:2020-12-28 难度:3 相似度:1.25

解析

纠错

下载

组卷

20160. （2021•漳州双语实验学校•四模）在平面直角坐标系中，抛物线L：y＝x²﹣2x﹣3与y轴交于点C，点D为抛物线的顶点．
（1）求点C、点D的坐标；
（2）将抛物线L向右平移m（m＞0）个单位得到抛物线L'，抛物线L与L'的交点为P，若△PCD是以CD为直角边的直角三角形，请求出m的值．

共享时间:2021-05-31 难度:4 相似度:1.25

解析

纠错

下载

组卷

20479. （2020•铁一中学•八模）如图，抛物线经过点A（4，4），B（5，0）和原点O，点P为抛物线上的一个动点，过点P作x轴的垂线，垂足为D（m，0）（m＞0），并与直线OA交于点C．
（1）求出抛物线的函数表达式；
（2）连接OP，当S_△_OPC＝

S_△_OCD时，求出此时的点P坐标；
（3）在直线OA上取一点M，使得以P、C、M为顶点的三角形与△OCD全等，请直接写出点M的坐标．

共享时间:2020-07-27 难度:4 相似度:0.83

解析

纠错

下载

组卷

23921. （2022•高新一中•二模）如图，已知抛物线y=-x²+bx+c与直线AB交于点A（-1，4），点B（3，0）．
（1）求抛物线的函数关系式；
（2）点M是x轴上方抛物线上一点，点N是直线AB上一点，若以B、O、M、N为顶点的四边形是以OB为边的平行四边形，求点M的坐标．
$德优题库$

共享时间:2022-03-14 难度:4 相似度:0.83

解析

纠错

下载

组卷

3119. （2018•遵义市•真题）在平面直角坐标系中，二次函数y＝ax²+

x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y＝﹣

x+2与二次函数图象在第一象限内的交点．
（1）求二次函数的解析式及点E的坐标．
（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．
（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．

共享时间:2019-06-03 难度:4 相似度:0.79

解析

纠错

下载

组卷

19062. （2016•交大附中•模拟）如图，已知抛物线C₁经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．
（1）求抛物线C₁的函数表达式．
（2）抛物线C₂与抛物线C₁关于原点成中心对称，求抛物线C₂的函数表达式．
（3）P是抛物线C₂上的第四象限内的动点，过点P作PM⊥x轴，垂足是M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

共享时间:2016-06-21 难度:4 相似度:0.75

解析

纠错

下载

组卷

21111. （2021•石狮市石光中学•九模）如图，在平面直角坐标系中，抛物线W₁：y=

x²+bx+c与x轴交于A（-4，0）、B两点，且过点C（0，-2）．抛物线W₂与抛物线W₁关于原点对称，点C在W₂上的对应点为C′．
（1）求抛物线W₁的表达式；
（2）写出抛物线W₂的表达式；
（3）若点P在抛物线W₁上，试探究：在抛物线W₂上是否存在点Q，使以C、C′、P、Q为顶点的四边形是平行四边形，并且其面积等于24？若存在，求点Q的坐标；若不存在，请说明理由．

共享时间:2021-08-10 难度:4 相似度:0.75

解析

纠错

下载

组卷

20185. （2021•西工大附中•五模）在平面直角坐标系中，经过点（1，﹣10），（2，﹣12）的抛物线y＝ax²+bx﹣6与x轴交于A、B两点（A点在B点的左侧），与y轴交于点C．
（1）求此抛物线的函数表达式；
（2）在抛物线确定一点P，使∠ACP＝90°，求点P的坐标；
（3）是否在x轴上存在点M，使∠OCM+∠ACO＝45°，若存在，求出点M的坐标；若不存在，请说明理由．

共享时间:2021-06-03 难度:4 相似度:0.75

解析

纠错

下载

组卷

20186. （2021•西工大附中•五模）问题提出
（1）如图①，在Rt△ABC中，∠ACB＝90°，AC＝BC．过点C作直线l，再分别过点A、B作AM⊥l于M，BN⊥l于N．则线段MN、AM、BN之间的数量关系为___________；
（2）如图②，在Rt△ABC中，∠C＝90°，AC＝30，BC＝40，点P在AB上，点E、F分别是边AC、BC上，且∠ABC＝∠FPB，PE⊥PF．设BP＝x，求四边形CEPF的面积y与x之间的函数关系式；
（3）如图③是一个圆形广场，其中四边形ACBD规划为园林绿化区（四个顶点均在圆上），且要求∠ACB＝90°，AC＝30米，BC＝40米，连接AB、CD交于点P．为了更好的美化环境，需要在AC、BC边上分别确定点E、F，且满足∠ABC＝∠FPB，PE⊥PF．为了整体布局，计划在四边形CEPF内种植花卉，在四边形ACBD剩余区域种植草坪．已知花卉每平方米的价格是60元，草坪每平方米的价格是90元，从实用角度希望四边形CEPF的面积最大．根据设计要求，求出当四边形CEPF的面积最大时种植花卉和草坪的总费用．

共享时间:2021-06-03 难度:5 相似度:0.75

解析

纠错

下载

组卷

1144. （2020•陕西省•副题）已知抛物线L：y=-x²+bx+c过点（-3，3）和（1，-5），与x轴的交点为A，B（点A在点B的左侧）．
（1）求抛物线L的表达式；
（2）若点P在抛物线L上，点E、F在抛物线L的对称轴上，D是抛物线L的顶点，要使△PEF∽△DAB（P的对应点是D），且PE：DA=1：4，求满足条件的点P的坐标．
$德优题库$

共享时间:2020-07-31 难度:4 相似度:0.58

解析

纠错

下载

组卷

4763. （2018••模拟）在平面直角坐标系xOy中，抛物线C：y＝x²+（3﹣m）x经过点A（﹣2，0）．
（1）将抛物线C沿直线y＝1轴对称的抛物线记为C₁，求抛物线C₁的顶点坐标；
（2）将抛物线C沿直线y＝n轴对称的抛物线记为C₂，设C与C₂的交点记为点M，点N，C的顶点记为F，C₂的顶点记为E，若四边形MFNE中有一个内角等于60°，求C₂的解析式．
$德优题库$

共享时间:2018-06-27 难度:4 相似度:0.58

解析

纠错

下载

组卷

848. （2014•陕西省•真题）已知抛物线C：y=﹣x²+bx+c经过A（﹣3，0）和B（0，3）两点，将这条抛物线的顶点记为M，它的对称轴与x轴的交点记为N．
（1）求抛物线C的表达式；
（2）求点M的坐标；
（3）将抛物线C平移到抛物线C′，抛物线C′的顶点记为M′，它的对称轴与x轴的交点记为N′．如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？

共享时间:2014-09-18 难度:3 相似度:0.58

解析

纠错

下载

组卷

21202. （2019•爱知中学•一模）如图，在平面直角坐标系中，点O为坐标原点，抛物线L₁：y=x²+bx+c经过A（1，0），且与y轴交轴点D（0，3）．
（1）求抛物线L₁的函数表达式；
（2）连接AD，将抛物线L₁绕平面内一个点M旋转180°得到抛物线L₂，其中A的对应点为C，D的对应点为B，若四边形ABCD是面积为20的矩形，求抛物线L₂的函数表达式．
$德优题库$

共享时间:2019-05-20 难度:4 相似度:0.58

解析

纠错

下载

组卷

gxyz515

2021-11-25

初中数学 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2021-2022学年陕西省西安市高新一中九上数学期中试卷

更新:2021-11-25 06:43浏览量:847

普通登录

手机登录

微信扫码立即登录