服务热线
试卷总分:120分 命题人:-1 考试时长:120分钟
，下列结论中不正确的是（ ）
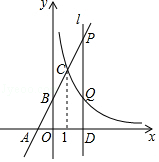
| A.其图象经过点（3，1） | B.其图象分别位于第一、第三象限 |
| C.当x＞0时，y随x的增大而减小 | D.当x＞1时，y＞3 |
（x＞0）、y=
（x＜0）的图象于B、C两点，若△ABC的面积为2，则k值为（ ）
图象上有三个点A（x1，y1）、B（x2，y2）、C（x3，y3），若x1＜0＜x2＜x3，则下列结论正确的是（ ）
的图象交于A，B两点，过A作y轴的垂线，交函数y=
的图象于点C，连接BC，则△ABC的面积为（ ）
（x＞0）绕原点O逆时针旋转45°得到的图形，P是曲线C2上任意一点，点A在直线l：y=x上，且PA=PO，则△POA的面积等于（ ）
（x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若△BCE的面积为4，则k= ．
（x＞0）的图象与正比例函数y=kx、y=
x（k＞1）的图象分别交于点A、B．若∠AOB=45°，则△AOB的面积是 ．
x与双曲线y=
（x＞0）交于点A，将直线y=
x向下平移个6单位后，与双曲线y=
（x＞0）交于点B，与x轴交于点C，则C点的坐标为 ；若
=2，则k= ．
的图象在第一象限的一个分支，点P是这条曲线上任意一点，它的坐标是（a、b），由点P向x轴、y轴所作的垂线PM、PN，垂足是M、N，直线AB分别交PM、PN于点E、F．则AF•BE= ．
（k≠0）的图象经过P，B两点，则k的值为 ．
，反比例函数y＝
的图象经过点C，与AB交于点D，若△COD的面积为10，则k的值等于_________.
的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k= ．
的图象在第一象限内交于点C（1，n）．
的表达式；
交于P、Q两点，且PQ=2QD，求点D的坐标．
x与双曲线y=
（k＞0，x＞0）相交于点A，将直线y=
x向上平移4个单位长度后，与y轴交于点C，与双曲线y=
（k＞0，x＞0）交于点B，若OA=3BC，求出双曲线的解析式．
（x＜0）的图象经过AO的中点C，交AB于点D．若点D的坐标为（﹣4，n），且AD=3．
的表达式；
（k≠0）过点A，点E（﹣2，m）、点F分别是反比例函数图象上的点，其中点F在第一象限，连结OE、OF，以线段OE、OF为邻边作平行四边形OEGF．
| 运行区间 | 成人票价（元/张） | 学生票价（元/张） | ||
| 出发地 | 终点地 | 一等座 | 二等座 | 二等座 |
| 甲地 | 乙地 | 56 | 36 | 30 |
2023-06-23
初中数学 | 测试 | 难度:3.26
word试卷生成中,请等待...
解析
收藏
下载
相似
组卷
