服务热线
搜题▪组卷
，
AB•CM＝
DAB•CD•sinα＝
absinα，
absinα；
AC•DE•sin60°＝
AC•DE，S△ABC＝
AC•BE•sin60°＝
AC•BE，
AC•DE+
AC•BE＝
AC（DE+BE）＝
AC•BD＝
×40×30＝300
（cm2）；
AC•DE•sinα，S△ABC＝
AC•BE•sinα，
AC•DE•sinα+
AC•BE•sinα＝
AC•（DE+BE）•sinα＝
AC•BD•sinα＝
absinα，
absinα；
•a•a•sin60°＝
•a•a•
＝
a2．
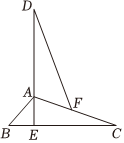
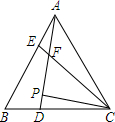已知：如图，△ABC为等边三角形，AE=BD，AD，CE相交于点F．
如图所示，A、C、B三点共线，△DAC与△EBC都是等边三角形，AE、BD相交于点P，且分别与CD、CE交于点M，N．
，她们继续深入探究了以下问题：
，
，求PD的长．
如图，AC平分∠BAD，CE⊥AB于点E，CF⊥AD交AD的延长线于点F，且BC=CD．
如图，△ABC是等边三角形，在直线BC的下方有一点D，且DB=DC，连接AD交BC于点E．
gxyz515
2021-11-25
初中数学 | 九年级上 | 解答题
纠错
收藏
下载
相似
组卷
如图，△ABC为等边三角形，E为BC边上一点，作CF∥AB，且CF=BE，求证：AE=AF．
解析
如图，在等边△ABC中，点D、E分别是CA、AB延长线上的点，且AD=BE．求证：∠ABD=∠BCE．
已知：如图等边三角形ABC中，D是AC中点，过C作CE∥AB，且AE⊥CE，求证：BD=AE．
如图，OA=OC，OB=OD，∠AOD=∠COB，试说明：AB=CD．
如图，已知∠A=∠D=90°，E、F在线段BC上，DE与AF交于点O，且AB=CD，BE=CF．求证：AF=DE．
