服务热线
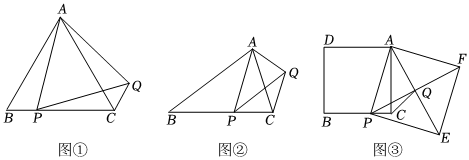
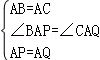 ,
, 声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/10/21 10:44:08;用户:黎艺明;邮箱:237845914@qq.com;学号:777974
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/10/21 10:44:08;用户:黎艺明;邮箱:237845914@qq.com;学号:777974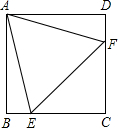
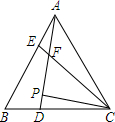 已知:如图,△ABC为等边三角形,AE=BD,AD,CE相交于点F.
已知:如图,△ABC为等边三角形,AE=BD,AD,CE相交于点F.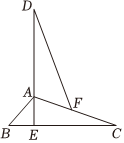

dyhz2022
2023-11-21
初中数学 | 解答题