已知：如图，在四边形ABCD中，AB∥CD，&ang;B=90&deg;，AB=6厘米，BC=8厘米，CD=10厘米，点P从点B出发，以2厘米/秒的速度沿BC向点C运动，同时点Q从点D出发，沿DC向点C运动，连接AP，PQ．则点Q的运动速度为&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;/厘米/秒时，△ABP与△CPQ全等．br /> i

首页 > 试题列表 > 单题解析

24216. （2021•交大附中•七下期中）已知：如图，在四边形ABCD中，AB∥CD，∠B=90°，AB=6厘米，BC=8厘米，CD=10厘米，点P从点B出发，以2厘米/秒的速度沿BC向点C运动，同时点Q从点D出发，沿DC向点C运动，连接AP，PQ．则点Q的运动速度为厘米/秒时，△ABP与△CPQ全等．
$德优题库$

共享时间:2021-05-06 难度:3

纠错

下载

相似

组卷

[考点]

全等三角形的判定直角梯形

[答案]

2或8．

[解析]

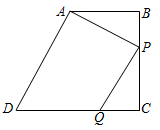
解：设点C运动t秒时，△ABP与△CPQ全等，
则BP=2t，
∵BC=8，
∴CP=8-2t，
∵AB∥CD，∠B=90°，
∴∠B+∠C=180°，
∴∠C=180°-∠B=90°．
①当AB=CQ=6，BP=CP时，△ABP≌△PCQ，
∴DQ=10-6=4，2t=8-2t，
∴t=2，
∴点Q的运动速度为4÷2=2（厘米/秒）；
②当AB=CP，BP=CQ时，△ABP≌△QCP，
∴8-2t=6，CQ=2t，
∴t=1，
∴CQ=2，
∴DQ=10-2=8，
∴点Q的运动速度为8÷1=8（厘米/秒）；
综上所述：点Q的运动速度为2或8厘米/秒时，△ABP与△CPQ全等．
故答案为：2或8．

[点评]

本题考查了"全等三角形的判定,直角梯形"，属于"综合题"，熟悉考点是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请告知发布者本人！