[答案]
(1)4;8;(2)①4或2;②﹣1;③存在,B对应的数为6;④存在,B对应的数为6,一定成立
[解析]
解:(1)|1﹣5|=|﹣4|=4,|﹣3﹣5|=|﹣8|=8;
故答案为:4;8;
(2)①设求知数为a,则有么|a﹣3|=1,即a﹣3=±1,
∴a=4或a=2,
故答案为:4或2;
②设求知数为b,则有|b﹣(﹣1)|=0,即|b+1|=0,解得b=﹣1.
故答案为:﹣1;
③设点C表示的数为x,则A表示的数为x+m或x﹣m,由题意可知m为栋梁距离,则m≥0,
设点B表示的数为y,则|m﹣y|=6,即m﹣y=±6,
∴m=y+6或m=y﹣6,则有:x+m=x+y+6.x﹣m=x﹣(y+6)=x﹣y﹣6,或x﹣m=x﹣(y﹣6)=x﹣y+6,
∴点A表示的数共有4种情况:a,x+y+6,b,x+y﹣6,c,x﹣y﹣6,d,x﹣y+6,
根据题意,其中两个值相同,并与另两个值都不同时,即可符合题意,
a﹣b得:x+y+6﹣(x+y﹣6)=12≠0,a≠b,同理c≠d,
当a=c时,x+y+6=x﹣y﹣6,2y=﹣12,得y=﹣6,此时a式为x+y+6=x,b式是x+y﹣6=x﹣12,c式是x﹣y﹣6=x.d式是x﹣y+6=x+12,
∵a=c,且与b、d式均不等,又m≥0,则y=﹣6时,m=y﹣6=﹣12不可取,所以四种情况中由m=y﹣6所得结果不可取,最多只有2个A点满足故y=﹣6舍去.
当a=d式时,有x+y+6=x﹣y+6解得y=0,则a:x+6,b;x﹣6,c:x﹣6,d:x+6,
a=d,b=c,则只有两个A点满足,故y=0舍去.
当b=c式时,x+y﹣6=x﹣y﹣6,解得y=0同上舍去;
当b=d式时,有x+y﹣6=x﹣y+6,解得y=6,则m=y+6=12>0,m=y﹣6=0,符合m≥0,此时,a:x+y+6=x+12,b,x+y﹣6=x,c,x﹣y﹣6=x﹣12,d,x﹣y+6=x,
则b=d,与a、c均不相同,对应一个确定的点C,即无论x取何值,都有且仅有三个点A满足条件,点A对应的三个数为x﹣12,x,x+12.
故存在唯一点B,B对应的数为6.
④由题意可知,设点C对应的数为x,B对应的数为y,则点A对应的数为x+m或x﹣m,m≥0,
又|y﹣m|=6,可得m=y+6或m=y﹣6,则条件与③相同,由③可知存在唯一点B,使题干条件成立.
故答案为:一定成立.
[点评]
本题考查了"有理数 数轴 列代数式 ",属于"典型题",熟悉题型是解题的关键。
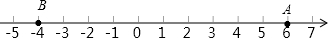


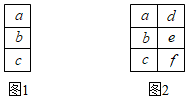 观察下列三行数:
观察下列三行数: