服务热线
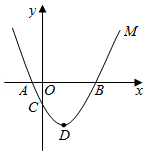
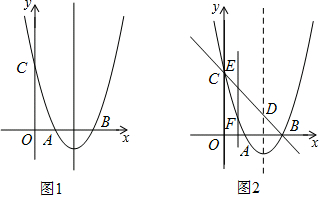
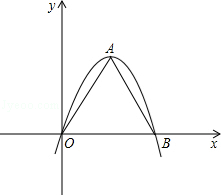
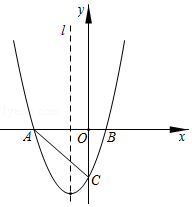
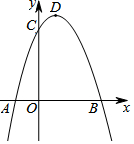已知二次函数y=ax2+bx-3a经过点A（-1，0），C（0，3），与x轴交于另一点B，抛物线的顶点为D．
，
，
×1×3+
（3+4）×1+
×（3﹣1）×4＝9；
×4×|﹣x2+2x+3|＝9，
，
，
，
，
，
，
，
时，y＝﹣（1+
﹣1）2+4＝﹣
，
时，y＝﹣（1﹣
﹣1）2+4＝﹣
，
，﹣
）或（1﹣
，﹣
）．
（x﹣h）2+
与抛物线M有一个公共点为E，则在抛物线N上是否存在一点F，使得以B、C、E、F为顶点的四边形是以BC为边的平行四边形？若存在，请求出h的值；若不存在，请说明理由．
x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．
分别交y轴，x轴于A，B两点，抛物线y＝﹣x2+bx+c过A，B两点，点M为直线AB上一个动点，过点M作x轴垂线交抛物线于点N．
，新的抛物线与y轴交于点E，点M是y轴上一点，点N是平面内一点，是否存在点M，N，使以点B，E，M，N为顶点的四边形为菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
如图，抛物线y=-x2+bx+c与x轴交于点A（-1，0），B（3，0），与y轴交于点C．
与抛物线y＝（x﹣3）2﹣4m+3交于A，B两点（其中点A在点B的左侧），与抛物线的对称轴交于点C，抛物线的顶点为D（点D在点C的下方），设点B的横坐标为t
CF的值最小，则满足条件的点F的坐标是 ．
已知抛物线L：y=ax2+bx+c（a≠0）与x轴交于点A（-2，0），点B（4，0），与y轴交于点C（0，4）．
tyz510
2021-11-15
初中数学 | 九年级上 | 解答题
纠错
收藏
下载
相似
组卷
解析
如图，抛物线y=ax2+bx+c与x轴交于点A（-1，0），点B（3，0），与y轴交于点C（0，3）．点M在线段OB上，ME∥y轴，交BC于点F，交抛物线于点E．