北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚，数学中也存在着神奇的&ldquo;黑洞数&rdquo;现象：br /> （1）请你用不同的三个数再试试，你发现了什么&ldquo;神奇&rdquo;的现象？br /> （2）请用所学过的知识现象解释一下（1）中的发现．br /> img alt="德优题库" src="/mat

首页 > 智能练考 > 在线答题 > 交卷详情 > 单题解析

23676. （2019•高新一中•七上期末）北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚，数学中也存在着神奇的“黑洞数”现象：
（1）请你用不同的三个数再试试，你发现了什么“神奇”的现象？
（2）请用所学过的知识现象解释一下（1）中的发现．
$德优题库$

时间:2022-01-17 难度:4

修改

相似删除

本地下载已共享

组卷

[考点]

规律型：数字的变化类

[答案]

答案详见解析

[解析]

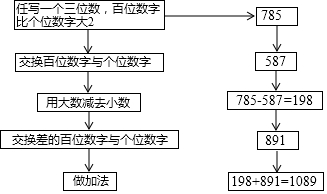
解：（1）任意三位数，百位数字比个位数字大2，
如：321
交换百位数字与个位数字：123
用大数减去小数：321-123=198，
交换差的百位数字与个位数字：891
做加法：198+891=1089．
发现了“神奇”的现象：结果都为1089；

（2）设任意三位数，百位数字为a，十位数字为b，个位数字为c，
则a=c+2，
所以三位数为：100a+10b+c=100（c+2）+10b+c，
交换百位数字与个位数字：100c+10b+a=100c+10b+（c+2），
用大数减去小数：100（c+2）+10b+c-（100c+10b+c+2）=198，
交换差的百位数字与个位数字：891
做加法：198+891=1089．
发现了“神奇”的现象：结果为1089．

[点评]

本题考查了"规律型：数字的变化类"，属于"难典题"，熟悉考点和题型是解题的关键。

相同试题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

dyhz2022

2022-01-17 18:20

初中数学 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2019-2020学年陕西省西安市高新一中七上数学期末试卷

更新:2020-02-17 07:56浏览量:748

普通登录

手机验证

微信扫码立即登录